Jumlah Rusuk Kubus Lengkap dengan Unsur hingga Rumus Kubus
- kelaspintar.id
VIVA – Jumlah rusuk kubus tentunya kita pelajari saat di bangku sekolah, khusunya dalam mata pelajaran matematika. Kubus sendiri pasti akan sering kita jumpai dalam kehidupan sehari-hari. Misalnya dadu dalam permainan monopoli dan ular tangga, kotak sepatu, kotak tissue dan benda berbentuk kubus lainnya.
Unsur semua bentuk kubus tentu akan sama, salah satunya titik sudut kubus. Dengan titik sudut kubus, kita bisa mendeskripsikan sebuah benda bisa dikatakan sebagai kubus dan begitu pula dengan unsur-unsur yang lainnya. Ada baiknya untuk kita pelajari terlebih dahulu tentang kubus sebelum mengetahui berapa jumlah rusuk kubus yang dihimpun dari berbagai sumber.
Titik Sudut Kubus dan Unsur Kubus
Kubus memiliki 6 unsur yang dapat mendefinisikannya sebagai sebuah bangun ruang. Lantas, apa saja unsur kubus tersebut? Berikut ini akan kita bahas mengenai maisng-masing unsur kubus.
1. Titik Sudut pada Kubus
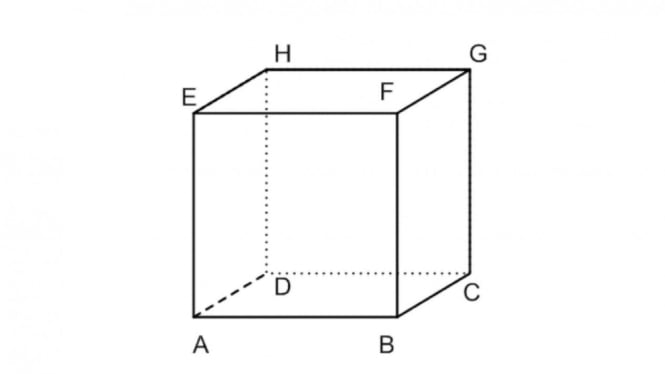
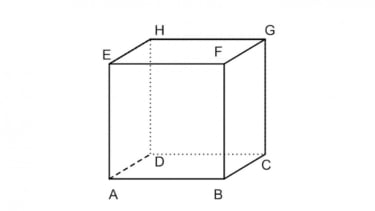
Titik sudut adalah titik potong yang berada diantara dua atau tiga rusuk. Pada gambar kubus ABCD.EFGH, bisa dilihat jika ada 8 sudut pada kubus ini yaitu A, B, C, D, E, F, G dan H.
2. Sisi pada Kubus
Sisi pada kubus adalah bidang yang membatasi kubus. Berdasarkan gambar kubus ABCD.EFGH di atas, didapati bahwa kubus adalah bangun ruang yang memiliki 6 sisi yang bentuknya sama yakni persegi.
Ke-6 sisi yang tertera pada gambar si atas diantaranya seperti berikut ini:
- Sisi bawah ABCD
- Sisi atas EFGH
- Sisi depan ABFE
- Sisi belakang DCGH
- Sisi samping kanan ADHE
- Sisi samping kiri BCGF
3. Rusuk pada Kubus
Rusuk pada kubus adalah garis potong yang berada diantara dua sisi kubus. Bentuknya terlihat seperti kerangka kubus. Berdasarkan gambar kubus di atas, jumlah rusuk pada kubus ABCD.EFGH ada sebanyak 12 rusuk.
- AB
- BC
- CD
- DA
- AE
- BF
- CG
- DH
- EF
- FG
- GH
- HE
4. Diagonal Bidang atau Diagonal Sisi Kubus
Dengan menarik garis pada masing-masing sudut kubus yang berhadapan setiap sisi atau bidangnya, maka berdasarkan gambar kubus di atas kita akan menemukan garis yang akan membentuk segitiga sama kaki. Garis inilah yang disebut sebagai diagonal bidang atau diagonal sisi kubus. Pada kubus ABCD.EFGH di atas, ada 12 diagonal bidang atau diagonal sisi yaitu:
- AF
- BE
- BG
- FC
- CH
- DG
- AH
- DE
- BD
- AC
- EG
- HG
5. Diagonal Ruang Kubus
Diagonal ruang merupakan dua titik sudut yang saling berhadapan dalam satu ruang. Berdasarkan gambar kubus ABCD.EFGH di atas ada 4 diagonal ruang yakni:
- BH
- DF
- AG
- EC
6. Bidang Diagonal Kubus
Sementara bidang diagonal terbentuk dari dua garis diagonal bidang dan dua rusuk kubus yang sejajar. 4 bidang diagonal yang ada pada kubus ABCD.EFGH yakni;
- ACGE
- DBFH
- ABGH
- EFCD
Jaring-Jaring Kubus
Ada banyak jaring-jaring kubus yang bisa dibuat. Seperti dua contoh gambar jaring-jaring kubus di atas.
Pada dua jaring-jaring kubus yang berbeda ini, sisi-sisi kubus yang saling berhadapan berwarna sama.
Jaring-jaring kubus tersusun dari 6 persegi yang sama (kongruen). Pada jaring-jaring kubus kedua dari I sampai VI.
Persegi I saling berhadapan dengan persegi IV, persegi II saling berhadapan dengan persegi V dan persegi III saling berhadapan dengan persegi VI.
Rumus Kubus
Pelajaran matematika tentunya tidak akan luput dari rumus yang selalu berdampingan dengan mata pelajaran ini. Rumus yang akan dibahas meliputi rumus luas permukaan kubus dan volume kubus.
Luas Permukaan Kubus
Coba perhatikan gambar di bawah ini.
Sebelumnya jaring-jaring kubus telah bahas. Nah, dengan jaring-jaring kubus tersebutlah nantinya kita bisa menentukan rumus luas permukaan kubus.
Seperti yang diketahui, kubus sendiri ntersusun dari 6 sisi yang bentuknya persegi. Dalam contoh ini misal panjang rusuk kubus adalah r, maka luas permukaannya yakni adalah:
Rumus Luas Permukaan Kubus:
Luas I = Luas II = Luas III = Luas IV = Luas V = Luas VI = Luas persegi
Luas persegi = r x r
Luas permukaan kubus = Luas I + Luas II + Luas III + Luas IV + Luas V + Luas VI
Lp = (r x r) + (r x r) + (r x r) + (r x r) + (r x r) +(r x r)
Lp = 6 x r x r = 6r2
Keterangan:
Lp : luas permukaan kubus
r : ukuran panjang rusuk kubus
Volume Kubus
Coba perhatikan gambar di bawah ini.
Contoh gambar di atas memperlihatkan kubus ABCD.EFGH dengan panjang rusuk r.
Volume prisma secara umum merupakan luas alas dikali dengan tinggi prisma.
Karena alas kubus bentuknya persegi dan panjang sisi r, maka luas alasnya adalah r2.
Rumus Volume Kubus:
Volume kubus = Luas persegi x tinggi
V = r2 x r
V = r3
Keterangan:
V : volume kubus
r : ukuran panjang rusuk kubus
Itulah penjelasan lengkap mengenai jumlah rusuk kubus beserta dengan titik sudut kubus dan unsur-unsur kubus. Mungkin memang pembahasanmengenai kubus ini terlihat sepele, tapi mungkin masih banyak yang belum mengetahui berapa jumlah kubus, titik sudut kubus dan apa saja unsur-usnur kubus. Maka dari itu dibuat pembahasan ini sebagai tambahan pembelajaran dasar pada kubus. Semoga tulisan ini dapat bermanfaat bagi kamu yang membutuhkan dan mempelajarinya.
Uji Kejelian! Bisakah Kamu Temukan Wanita yang Tersembunyi dalam Gambar?
Ilusi optik selalu menjadi daya tarik bagi banyak orang, terutama saat memberikan tantangan unik yang melibatkan fokus dan kemampuan observasi.
