- VIVA/Agus Setiawan
VIVA – Rumus luas lingkaran sangat mudah untuk dipelajari. Nah, buat kamu yang belum mengetahui rumus lingkaran, simak ulasan selengkapnya berikut ini ya.
Lingkaran adalah salah satu bangun datar dalam materi pelajaran matematika. Dalam soal matematika menghitung luas lingkaran salah satu pertanyaan yang sering muncul.
Sebelum mempelajari rumus menghitung luas lingkaran, mari kita pelajari pengertian dasar lingkaran. Lingkaran merupakan tempat kedudukan titik-titik yang berjarak sama dengan satu titik tertentu. Titik tertentu adalah titik pusat lingkaran. Sedangkan jarak yang sama adalah jari-jari lingkaran.
Sebagian orang mungkin merasa bahwa menghitung luas lingkaran itu sangat sulit, tidak semudah menghitung luas persegi ataupun persegi panjang.
Ada banyak cara yang dapat digunakan untuk menentukan luas sebuah lingkaran, asalkan nilai salah satu bagian lingkaran tersebut diketahui. Seperti contoh panjang jari-jari, panjang diameter, keliling, ataupun luas juring. Setelah itu, kamu hanya perlu menggunakan rumus luas lingkaran.
Untuk menentukan luas lingkaran, kamu perlu mengingat nilai konstanta ?. Nilai ? dengan 20 desimal yaitu 3,14159265358979323846. Namun pada umumnya, nilai ? yang digunakan hanya dua desimal saja, yaitu 3,14. Selain itu, nilai ? juga dapat dituliskan dalam bentuk pecahan, yaitu 22/7.
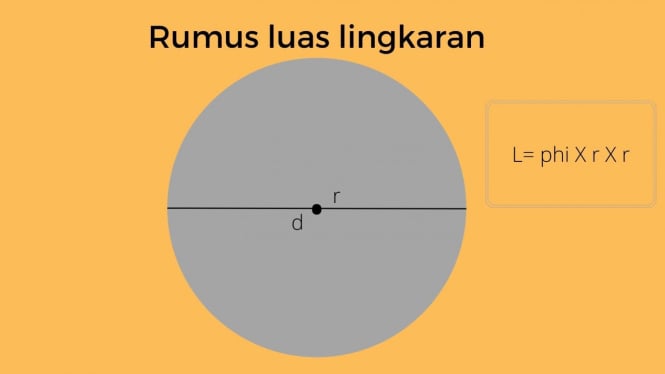
Rumus luas lingkaran
Berikut adalah rumus luas lingkaran yang dihitung dengan menggunakan jari-jari, diameter, keliling, hingga luas lingkaran.
1. Jari-jari lingkaran
Jika panjang jari-jari lingkaran diketahui dalam soal, maka luas lingkaran dapat ditentukan dengan rumus L= phi x r². Kuadratkan panjang jari-jari, kemudian di kalikan dengan konstanta phi. Contoh panjang jari-jari lingkaran adalah 8 cm, maka luas lingkaran tersebut adalah L= phi (8)²= 64 phi, atau 200,96 cm2.
2. Diameter lingkaran
Terkadang, ada beberapa soal yang tidak memuat informasi panjang jari-jari, tetapi hanya memuat informasi tentang panjang diameter (d). Penting untuk diketahui dan dipahami, bahwa diameter lingkaran yaitu dua kali jari-jari lingkaran. Maka, dapat diperoleh rumus d = 2r <=> r = 1/2d.
Substitusikan r = 1/2d ke dalam rumus luas lingkaran sehingga dapat diperoleh L= phi r² = phi (1/2d)² = 1/4phi d² Dengan demikian, luas lingkaran dapat dihitung dengan menggunakan panjang diameter (d) yang rumusnya adalah L=1/4 phi d²
3. Keliling Lingkaran
Untuk menghitung luas lingkaran dari keliling lingkaran, kamu harus menentukan panjang jari-jari lingkaran terlebih dahulu. Panjang jari-jari lingkaran dapat ditentukan dari rumus keliling lingkaran K = phi x d = 2 x phi x r sehingga r = K/2 xphi.
Setelah itu, gunakan rumus luas lingkaran untuk menentukan luas lingkaran.
4. Luas Juring
Dalam beberapa soal, luas lingkaran juga dapat ditentukan dengan luas lingkaran. Lingkaran adalah bagian dari lingkaran yang dibatasi oleh dua jari-jari dan busur. Garis tersebut berbentuk seperti potongan pizza dan memiliki sudut tengah dengan bagian tengah sebagai simpul.
Besarnya sudut ini dapat diukur dengan menggunakan busur derajat, dan dalam satu putaran penuh, sudut pusatnya adalah 360 derajat. Luas lingkaran dapat ditentukan dengan membandingkan besar sudut pusat busur dengan sudut satu lingkaran penuh.
Jika kamu mengetahui luas dan sudut pusat, kamu dapat menggunakan rumus berikut untuk menghitung luas lingkaran. Luas lingkaran = alpha/3600 x L, dimana alpha adalah sudut pusat dalam derajat.
Contoh Soal Menghitung Luas Dan Keliling Lingkaran
Untuk memudahkan kamu dalam menghitung, berikut telah kami rangkum contoh soal menghitung luas dan keliling lingkaran yang melansir dari rumusrumus.
Contoh Soal 1:
Jika diketahui sebuah lingkaran memiliki diameter 14 cm. Berapakah luas lingkaran tersebut?
Penyelesaian:
Diketahui:
d = 14 cm
karena d = 2 × r maka:
r = d/2
r = 14/2
r = 7 cm
Ditanyakan: Luas lingkaran?
Jawab:
Luas = p × r²
Luas = 22/7 × 7²
Luas = 154 cm²
Jadi, luas lingkaran tersebut adalah 154 cm².
Contoh Soal 2:
Sebuah lingkaran mempunyai jari-jari sebesar 10 cm. Berapakah luas lingkaran tersebut?
Penyelesaian:
Diketahui:
r = 10 cm
Ditanyakan: Luas lingkaran?
Jawab:
Luas = p × r²
Luas = 3,14 × 100
Luas = 314 cm²
Jadi, luas lingkaran tersebut adalah 314 cm².
Contoh Soal 3:
Hitunglah keliling lingkaran dengan jari-jari 20 cm.
Penyelesaian:
Diketahui:
r = 20 cm
p = 3,14
Ditanyakan: Keliling lingkaran?
Jawab:
Keliling = 2 × p × r
Keliling = 2 × 3,14 × 20
Keliling = 125,6 cm
Jadi, keliling lingkaran tersebut adalah 125,6 cm
Unsur-unsur dalam sebuah lingkaran
- Titik pusat lingkaran yaitu titik yang berada di tengah-tengah lingkaran.
- Jari-jari lingkaran adalah garis yang menghubungkan antara titik pusat dengan titik lengkung pada keliling lingkaran.
- Diameter lingkaran yaitu garis panjang lurus yang menghubungkan antara dua titik pada keliling lingkaran yang melewati titik pusat lingkaran.
- Tali busur lingkaran adalah garis lurus yang menghubungkan dua titik pada keliling lingkaran, tapi tidak melalui titik pusat lingkaran. Berbeda dengan diameter yang garisnya melalui titik pusat.
- Juring lingkaran yaitu luas daerah dalam lingkaran yang dibatasi oleh dua garis jari-jari dan dibatasi oleh sebuah busur lingkaran yang letaknya diapit oleh dua buah jari-jari tersebut.
- Keliling lingkaran adalah luas lingkaran yang dibatasi oleh busur dan tali busur.
- Titik puncak lingkaran adalah jarak terpendek antara tali busur dan pusat lingkaran. Garis apotema biasanya tegak lurus terhadap akord.
- Busur adalah kurva yang merupakan bagian dari keliling lingkaran. Ada dua busur dalam lingkaran, busur besar dan busur kecil.
- Sudut pusat adalah sudut antara dua jari-jari di pusat lingkaran.
- Sudut keliling lingkaran adalah sudut yang dibentuk oleh perpotongan dua tali busur dengan sebuah titik pada keliling tersebut.
Demikian ulasan tentang rumus luas lingkaran lengkap dengan contoh-contohnya. Cara di atas adalah rumus-rumus mudah dalam menghitung luas lingkaran. Semoga artikel ini dapat membantu dan bermanfaat.
Kalahkan 11 Negara, Siswa Indonesia Sabet Emas Kompetisi Matematika Internasional di Australia
Selain juara kompetisi matematika internasional, siswa Indonesia lainnya juga berhasil meraih medali emas di kompetisi Bahasa Inggris bagi pelajar dari berbagai negara.
